Fillet-weld test evaluation

Introduction

Abbreviations used

January2021 - the new data and interpretations presented here come from the series of four mini-projects, three in November 2020 and one in January 2021, abbreviated as follows:

Butt-welds - not part of this topic:

• mp1 = 1st mini-project - "U-weldment in R.H.S. - fabricate, analyse, test"
• mp2 = 2nd mini-project - "Weld test - weld at centre of simply-supported beam"

For the fillet welds tests:

• mp3 = 3rd mini-project - "Fillet welds tensile tested in beam test"
• mp4 = 4th mini-project - "Tensile-test rig for beam-configuration fillet-weld samples"

Other abbreviations used:

• bcfwtt = Beam-Configuration Fillet-Weld Tensile Test
• RHS = Rectangular Hollow Section
• FEA = Finite Element Analysis

Content

This page collates

• findings and data
• interpretation of these

• own tests
• own FEA
• other works where helpful to develop own analyses

At time of creating this page, late January2021, own content may include

• interpretation of tests performed November2020 to January2021
• reference to fatigue-resistant fillet-welds programme Summer2011
• possibly some fillet-weld tests looking at weld quality assurance 2014

Context

At time of writing, January2021, the major interests are

• harnessing the fillet-weld "static" tensile break test method "as is" to understanding fillet-weld "static" loading performance
• developing the fillet-weld test method as a "dynamic" loading method for investigating fatigue-resistance / cyclic-load performance of fillet welds
• applying these to Proposal : research path to high-strength steel fatigue-resistant welded structures utilising the 2011 observation that fillet-welds can perform in fatigue near the "mill" steel sections they are joining

Previous investigations and findings

Fillet-weld fatigue-resistance investigation 2011

From 2011 - fatigue-resistant fillet welds test programme -"index" page to the methods, tests and interpretations of a programme investigating the possibilities for fatigue-resistant fillet welds for warships and bridges.
Also as report [PDF, 3.2MB]. Interesting result - FCAW T-fillet 1.4Million cycles unbroken no cracks detectable, for 250thousand cycles expected to break. Which could now be progressed if the "bcfwtt" could be made cyclic loading for fatigue testing. Considered in Proposal : research path to high-strength steel fatigue-resistant welded structures

The beam-configuration fillet-weld tensile test findings

These are mp3 and mp4 of the Nov2020-to-Jan2021 test programme.

Necessary data from the beam-configuration fillet-weld tensile test to enable calculating the force on the test-weld are

• hydraulic piston force at moment the sample broke
  (typically a "Force=Pressure*Area" estimate using
  • hydraulic fluid pressure at moment of breakage
  • the hydraulic cylinder's piston diameter
  where piston-area=pi.d^2/4)
• The separation of the beam's bearers from the central plate ("L_m-a")
  (where 2*L_m-a + central-plate-thickness = separation of the two bearers)
• the height of the beam section ("h")

• the size of the test weld(s) - typically the leg-length ("z" in standard welding terminology)
• the length of the test welds

• the welding conditions
• the material specification of the weld(s)
• the material specification of the two half-beams

In the "bcfwtt", to obtain the force in the weld at breaking F_w (which we want) from the force applied by the hydraulic piston F_p (which we know) uses the formula
F_w=-F_p*L_m-a/2h
which is probably what one would intuitively guess.
Whose derivation is presented in mp3 see section Stresses in weld analysed .

Data and its processing

"Fillet welds tensile tested in beam test" [mp3]

The measurements and analysis are presented in the web-page for mp3

For the [ISO14341-A] "G3Si1" weld-metal, the calculated breaking strength is 567MPa - for expected typical value for "G3Si1" weld-metal of 560MPa.

"Tensile-test rig for beam-configuration fillet-weld samples" [mp4]

The hydraulic pump-and-cylinder used in mp4 had no hydraulic-fluid pressure-gauge, so an accurate citable "F=P.A" estimate of cylinder force applied to the test sample is not available.

An estimate of force applied was made by a very inexact method described. But where the resulting deduced weld breaking stress could not be known at the time of the test. So there could be no human bias in the applied force estimate.

The resulting fillet-weld breaking strength estimate of 572MPa, for the expected 560MPa mean value for "G3Si1" GMAW/MIG weld metal, is surprising for its apparent accuracy.

Evaluation and interpretation of tests

Writing Thursday 28January2021:

• the tests, despite being done apparently rather approximately, present estimates of weld strength in MPa - the stress they bear at breaking - which are remarkably close to the accepted typical 560MPa break-strength of a "G3Si1" ("ER70s-6") GMAW/MIG weld
• the appearance of the broken welds are presented in fillet-weld fracture pictures
• the weld fracture surfaces in this "static" (ie slowly increasing) overload are apparently ductile "microvoid coalescence" fracture - judging by the very finely rough grey appearance
• the observed fracture orientation of the test fillet welds accords with the observation(s) of the practically experienced Hicks (ref.) in his book, see pg82, being along or close to the fillet leg between weld and the plane of the longitudinal beam surface
• the deduced value for weld fracture stress does match the established expectation - but my derivation is different, being simpler and is based on the observed mode (myself, Hicks (ref.)) of fracture (developed further imminently)
• in that the familiar tensile fracture strength of the weld (not the shear strength, which would be half of the uniaxial tensile strength) is output by dividing the force upon the weld at moment of break by {weld-leg-length * weld-linear-length} (the area of the fractured fillet "leg")

• the following two main findings are significantly made by this one image - FEA output - von Mises stress which can be identified in the referenced webpage on FEA of the "bcfwtt" (stress scale example - "1.001E+09" = 1.001GPa / 1001MPa)
• the location and orientation of weld overload fracture expected by FEA concurs with the physical outcome of own observations and Hicks (ref.)
• at the force known in the physical test to cause fracture FEA shows the intensity of stress in the weld appears enough to cause fracture

More detailed interpretation of fillet-weld tensile break measurements

The findings can now be considered in relation to established knowledge and theory.

Concepts and terminology:

- as I visualise them, from mp3

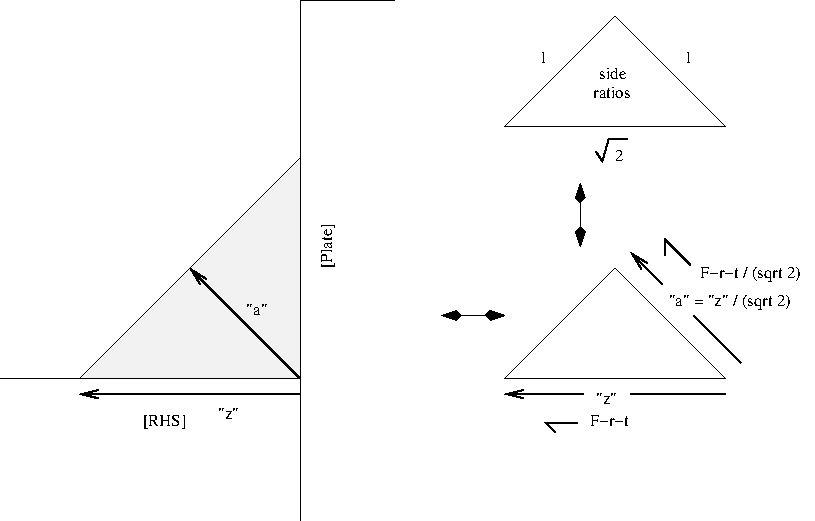
- as visualised by Hicks (ref.) on pg85

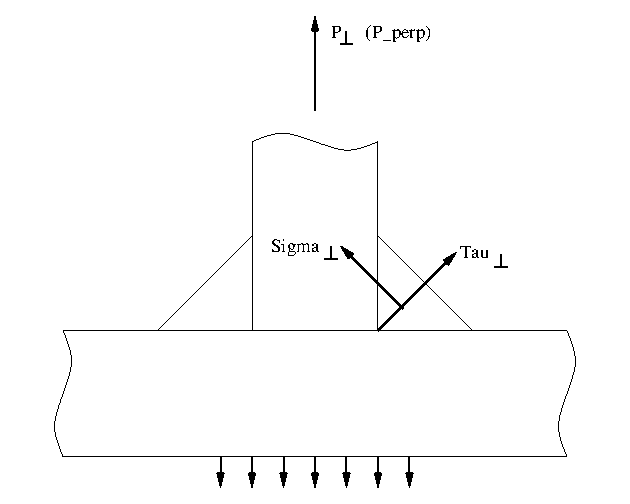
where Sigma=linear-stress and Tau=shear-stress.

Hicks (ref.) on pg85 presents the known established formula which should connect
strength[MPa]<->force[N]
for a *double-sided* fillet weld

In this equation he presents as [6.3],
with symbols here given text name
P_perp=2.t.L/sqrt2 * (sigma_perp+tau_perp)
and introducing t=fillet throat thickness ("a" in common welding terminology) and L=length of the weld

Taking [6.3] and [6.4]
P_perp=2.t.L/sqrt2 * (sigma_perp+tau_perp)
and
sigma_perp = tau_perp {for this geometry}
plus;
we recognise for a 45-45-90 triangular cross section fillet that "t", the weld throat, which is "a" in conventional weld terminology - that sqrt2.a=z - the fillet leg-length
so
sigma_perp=P/(2.sqrt2.t.L)=P/(2.z.L)

This is for a *double-sided* fillet weld.
Mine has two welds, but in series, not in parallel.
Each weld must take the full stress - so it is in stress terms a single-sided fillet weld ("ssfw").
So in my case of applying "Hicks"
sigma_perp_ssfw=P/(z.L)
which is the same as what I found empirically and in forming mathematics which matches the physical situation. The observation that fracture is along the longitudinal leg (length "z") of the fillet weld.

"My" derivation for fillet weld strength and the established arithmetic expression for fillet weld strength give the same answer.

So, to that extent, my "finding" is "expected".

Whereas the mode of breakage differs, with my derivation expecting fracture along the longitudinal fillet leg, and the established expression implying fracture is expected across the weld throat.

Hicks qualitatively comments, on pg82, that fillet weld overload fracture has the form which I found - close to the longitudinal fillet leg. So he's derived and presented "the established" analysis in that knowledge.
So it "doubly" affirms that the derivation applies.

I invite comment on these following things which I find surprising:

• I know the shear yield is half the observed uniaxial tensile yield - and you'd expect that to largely carry-over into break-stress - so I was kind-of expecting a breaking force half of what's observed, given the argument that this loading looks like pure shear and you'd expect to see a lower break strength from more "efficient" loading on the weld metal to induce overload failure ?
• WRONG !!! -> "why doesn't the "S355" substrate material with nominal 355MPa yield manifest as the strength, given the proximity of the fracture around the weld-metal||plate-metal boundary?"
• The 355MPa is the yield stress on distributed-deformation bending - as seen when the beam bends - as observed in own butt-weld tests mp1 and mp2
• Is the break strength of S355 steel in local break constrained to no distributed deformation 560MPa ?
• Is the FEA simulation's ( image , webpage ) full span of weld leg but very narrow high stress zone - about 1.5mm width at above 1GPa - such constraint against yielding ?
• Would a "macro" of the break region (section and smooth to fine abrasive (eg "800 grit") then etch with eg iodine etchant and examine) show whether the break is through the weld metal or "parent metal" of the RHS ? ( example of a "macro")

References