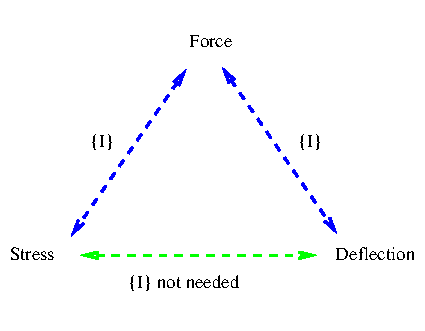
stress<=>deflection equations have been derived for two cases:
The simple derived equations are for symmetrical beams only - eg I-beams; Rectangular Hollow Sections and Square Hollow Sections.
The derivations are mathematically trivial. The engineering applications explained in the rest of the page give them significance. The derivations, typeset as PDF's
Having not welded or been involved in engineering for a while, these equations emerged from a leisure moment rather like doing a "crossword" puzzle or a "Sudoku" puzzle.
In these equations for stress<=>deflection, the Second Moment of Area I cross-cancels and beam height is the only section geometric characteristic needed.
One significance is design information is unnecessary when applying these equations.
Explained in a different way...
To calculate I needs a complete description of the
cross-sectional form of the beam - thicknesses of the various parts,
widths, heights, positions, etc. Which is design information.
Without design information, accurate measurement were it possible
could provide all needed information - to identify a commercial
section whose I is known, or to calculate I. If in
the service application there is no access to at least one end of the
beam section these might be difficult to measure.
So when presented with an in-service beam it is advantageous to
have an applicable equation which does not contain I.
Which is provided here by the stress<=>deflection equations, where
fortuitously the I's have cross-cancelled and disappeared from
the equations.
Shown diagrammatically here...

Is this already known?
My instinct is yes - the path I trod to these equations is obvious and instinct would lead others to find the same derivation - which is mathematically trivial.
I have not found existing use of these equations - but neither would I know where to look, being a welder and metallurgist by background.
An engineer in North America knows and has used this practical crucial point that with a string and tape-measure you can obtain the stress in a beam - but did not know of the "direct calculation path" shown green in the above diagram. He used online beam calculators in sequence to go from deflection to force then force to stress - both needing I.
For what it's worth - the original webpages as the project grew
There is some helpful explanation in the first, "simply-supported-beam central-load", webpage on pragmatic application to steel beams.
Coming back from the explanations and derivations for the SSB-CL and SSB-UDL cases; one application presented is a checking analysis that an in-service beam is acceptably loaded. Say you are walking around
These show the readily-made measurements necessary to deduce the stress in an in-service beam:
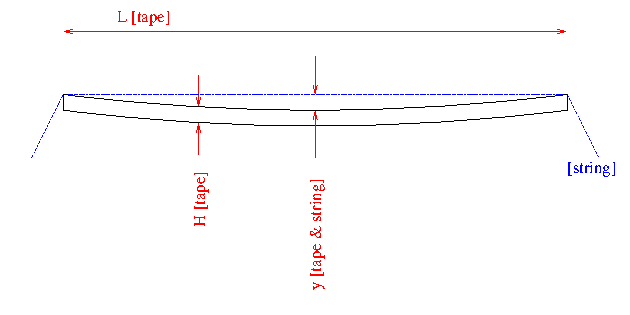
If the beam is steel the value of the elastic modulus E is needed and is fairly invariant for all common situations, at about 210GPa.
Many applications will not be at the pure "extreme" of being centrally loaded, nor purely at the least "severe" case of uniformly distributed load.
For example a bin with a discharge chute for loading lorries (trucks) is on about the middle half of the beam... It is midway between centrally loaded and a uniformly distributed loading.
There is an expedient way to proceed which in most instances will conclude the analysis on finding the beam loading is acceptable. Given the structure is most likely correctly designed for the current application.
The equations have identical form for the "centrally loaded" and the "uniformly distributed loaded" cases. With "only" a quarter difference in the constants and therefore the answers.
Applying the centrally loaded version is always "conservative" (ie to the safe side) when analysing if the stress is acceptable. So in an "impure" case of how the loading applies, that expedient strategy is to apply the simply-supported-beam central-load (SSB-CL) formula. If that calculated answer would be an acceptably low stress, the conclusion can be drawn that the beam loading is acceptable and the analysis concluded favourably.
The difference is a quarter (25%).
In such a case of a high service stress being found there would almost
certainly be far bigger concerns - eg
(R. Smith, 06Nov2023 to 07Nov2023)