For an engineeringly important case whose real-world behaviour I have direct experience of, I investigated "convergence" of Finite Element Analysis models for local stress-raising features vs their geometry.
This page is to be read given this background .
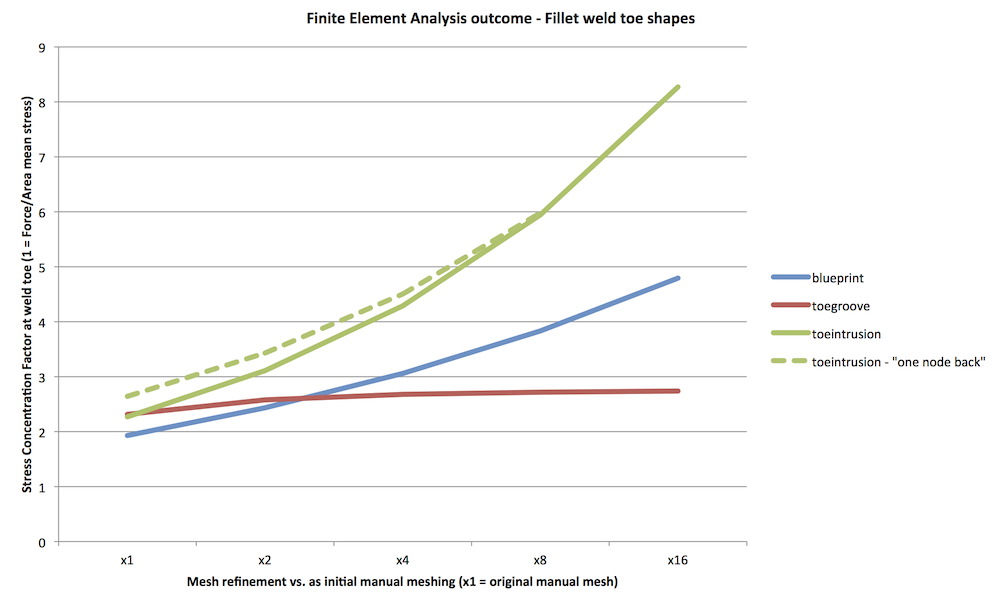
The outcome of the endeavour is conveyed in entirety by the following graph:
(also
presented here
in PDF format)

Explaining the graph lines as follows:
In an ideal world, all the lines would be horizontal: the predicted
stress concentration factor would always have a single constant value.
However, Finite Element Analysis is an approximate method. The
predicted answer(s) will more closely match the actual answer(s) as
discretisation / mesh-refinement increases. That's "convergence".
However, some models won't "converge". They "diverge".
Investigating this is the purpose of this page.
Even the "wide" 135deg angle of the fillet weld toe of the "blueprint" case defies convergence, with ever-rising stress-concentration with increasing discretisation / mesh-refinement.
The "toe intrusion" case, which is effectively a crack, has the
steepest upward slope, representing the most rapid divergence with
increasing mesh refinement. As expected for a crack and a general
linear-elastic finite element model, the predicted peak stress rapidly
becomes larger with mesh refinement.
The dashed second line for this case shows a physically incorrect
output of the finite element analysis model - where highest stress is
not at the crack tip (physically it definitely is!), but back from the
crack tip on the plate (not weld) side.
This is shown in eg the coarse manual-meshed
model of stresses around fillet weld toe-intrusion
.
As discretisation / mesh-refinement increases, the maximum stress
predicted does move to the crack tip - hence the termination of the
dashed line. At least this is physically correct...
The "toe groove" case does converge.
It settles to a value of 2.7 stress-intensification factor with
increasing mesh refinement.
Established engineering knowledge suggests this is reasonable. The
peak stress concentration around any cylindrical ("drilled") hole in a
large plate in tension along its length is x3.
(search on "stress intensity factor hole plate" eg
[external link]
image and analytical derivation)
That the "toe groove" case does converge in the FEA model appears to
be, in itself, a concordance with a physical reality.
Welding-specific explanation - "toe groove" is misnamed "undercut" and
is considered a flaw - and can be classified as a "rejectable defect"
(ISO 5817:2007 "Welding - Fusion-welded joints in steel, nickel,
titanium and their alloys (beam welding excluded) - Quality levels for
imperfections"; types "5011" (Continuous undercut) and "5012"
(Intermittent undercut))
Returning to the fundamental argument; borderline toe-groove and
modest toe-groove are associated with excellent fatigue-resistance.
Fatigue endurances found on test can be much higher than for the
general case of fillet welds, which tend to be very low and "pessimum"
regarding fatigue-resistance. The only plausible explanation is that
the stress-concentration (stress intensification factor) at the weld
toe when bordeline-to-modest toe-groove must be lower than for the
"perfect weld mitre" (sic) case.
The author's own investigation is presented as
"Improving fatigue performance of steel T-joint welds - a pilot study"
, with specific treatment of this topic is Section 4.3.4.
Figure 4.1 conveys my own impression of where the optimum is found
- that borderline to modest toe-groove may prove to be optimum;
contrary to current orthodoxies.
The concordance between the physical world and FEAm is that the smooth
shape of the weld toe with modest toe-groove is "well-behaved"
regarding stresses, and produces the lowest stress intensification
factor practicable for a weld toe.
So, in summary:
"chasing" convergence with mesh refinement shows that my models of
local weld toe geometries do accord with observed physical
behaviour - when an interpretation stage is applied to "divergent"
cases between specific numbers output and conclusions reached.
(R. Smith, 14Aug2017, 31Aug2017, 21Sep2017)