
[Wikipedia]
the balance of
Force of gravity (constant) vs Force of fluid drag (increases with velocity)
This application of Stokes' law [Wikipedia] assists in an unseen but legitimate way in a particle-size-analysis by sieve-analysis.
One can visualise Stokes' model:

In July 2025 I did this comminution and particle-size-analysis which gave this particle-size-distribution graph:
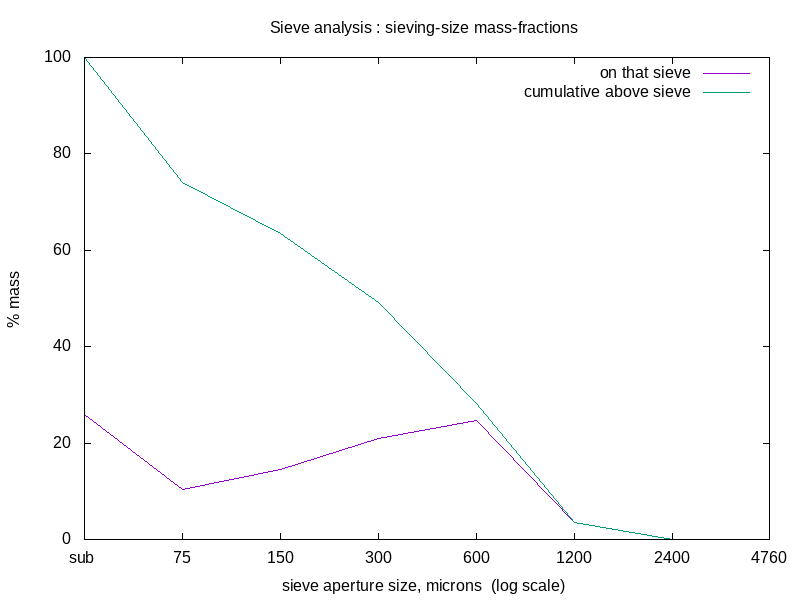
The mass fraction of sub-sieve fines is notable, at 26%.
Why they are there is another issue not considered here.
That they are there and cause problems while doing the
particle-size-analysis by sieve-analysis is what I address here.
What I actually did, in the name of sieve-analysis, was to
use sedimentation to pre-separate as much as possible of the
very-fine sub-sieve mass-fraction.
I managed to separate 83% of the sub-sieve very-fines - 21.5% of the
total mass of comminute - by a sedimentation method.
Those 841g of very-fines were passed through the finest, 75micron, sieve during the sedimentation, with no effect, but the primacy of sieve-analysis was maintained.
The large fraction of fines cause clogging-up of the sieves during
attempted sieving.
More exactly to say: with the fines removed none of the clogging of
the sieves which had been a problem when the fines were there were
encountered.
Noting:
the first sieving must be a wet sieving removing sub-sieve fines
which, dry, would float in the air and if angular silica particles are
a severe hazard to health.
That water with the fines in combination are probably what causes
clogging of the sieves.
By "clogging" what is meant that a thick immobile layer builds up on a
sieve, where of the "clogging" mass much is finer than the sieve
aperature and should pass through that sieve.
However:
by removing the very-fine "sub-sieve" particles by another process,
the sieving can be all dry sieving - which is quicker and easier
certainly in this case.
Tip the comminute into a trug (flexible tough builder's bucket)
half-filled with water.
Stir.
Bring water to a stop.
Leave a time - in seconds - for the heavier particles to sediment
towards the bottom of the trug.
Ladle the liquid from the near-surface, through the finest sieve (do
it right and you catch nothing - the opaque liquid goes straight
through) to enforce the primacy of the sieves in this declared
sieve-analysis, into another trug.
Add more water to the "with-comminutes" trug where necessary - get
very fines extracting into new water, until the amount of fines is
becoming minimal.
All the very-fines should end-up in the second trug.
"Stir" can be with a stick - but much more effective is a plaster-mixer spun by a drill; especially as reversing the drill for a moment can bring the water to an abrupt stop, no motion.
I already knew of Stokes' law [Wikipedia] and "Stokes terminal velocity", which are the basis of sedimentation.
While developing the "reverse sedimentation" ("reverse" because you are taking what does not sediment) empirically, I was guided by knowing of Stokes Law and knowing of the proportionalities which should, and did, make the technique work.
I did my usual working : developing a text-file with my notes, calculations done by expressing maths in the language of the text-processor's interpreter for most of its functionality, and answers to those calculations inserting into the file for the human to see.
For brevity, I get straight into that "working".
"Lisp" uses a prefix notation.
"Obvious" examples to convey the overall idea:
(* 4 3 2 1)is 24
(/ 24 2 3)is 4
Firstly the mathematical basis as "defuns" - with some arbitrary maths-only tests that the functions give the expected output:
Anything to the right-hand-side of a ";" is a comment - solely for the human.
;; the equation in wikipedia
;; https://en.wikipedia.org/wiki/Stokes%27_law
;; v = 2/9 . (rho_p - rho_f)/eta . g r^2
(defun stokes-velocity
(rho-particle rho-fluid dynamic-viscosity acc particle-radius)
"trusting wikipedia on this one; given units check yes; note particle *radius*"
(*
(/ 2e0 9)
(/ (- rho-particle rho-fluid) (float dynamic-viscosity))
acc (expt particle-radius 2)))
;; (* (/ 9 2e0) (stokes-velocity 0.6 0.1 0.5 10 2)) ;; 40.0 ;; yes
(defun stokes-velocity-pdia
(rho-particle rho-fluid dynamic-viscosity acc particle-diameter)
"to stokes velocity using particle *diameter*"
(stokes-velocity rho-particle rho-fluid dynamic-viscosity acc (/ particle-diameter 2e0)))
;; (* (/ 9 2e0) (stokes-velocity-pdia 0.6 0.1 0.5 10 4)) ;; 40.0
Created some values as named variables, so the meaning of subsequent calculations is obvious on inspection:
;; the values used: (setq dens-silica 2700 ;; is density of silica (to a good approximation), kg m^-3 dens-water 1000 ;; is density of water, kg m^-3 visc-water 1.0016e-3 ;; = 1.0016x10^-3 = dynamic viscosity of water grav-earth 9.81 ;; is gravity on Earth - m s^-2 or N kg^-1 (interchangeable units) sec-per-min 60 ;; will be seconds/minute mm-per-m 1000 ) ;; in fn. stokes-velocity-pdia the last number, many 75e-6, is the ;; particle *diameter* in metres (m) ;; 75micron is smallest sieve size, currently - hence my "sub-sieve" ;; is sub-75micron, and 75micron is the crucial size re. sedimentation.
Start doing some calculations; "getting a feel for" the values offered:
(stokes-velocity-pdia dens-silica dens-water visc-water grav-earth 75e-6) ;; 0.005203237320287538 ;; m s^-1
So for 75micron size particles, if they were of the idealised spherical shape (caveat to keep in mind), that is 5.2mm per second descent through water pulled by Earth's gravity.
(* (stokes-velocity-pdia dens-silica dens-water visc-water grav-earth 10e-6) ;; 9.250199680511183e-05 ;; m s^-1 mm-per-m sec-per-min) ;; 5.55011980830671 ;; mm per minute
What doesn't convey well to an audience - I tried different particle sizes, looking at the answers, seeking a threshold value - which I found:
;; if ladle from the top 50mm after 6s... ;;#;; this vvv -- played with diameter until found answer -> is 95micron (* (stokes-velocity-pdia dens-silica dens-water visc-water grav-earth 95e-6) mm-per-m 6) ;; 50.089831269968045 ;; mm ;; there you have it - 6s will just catch +75microns
So have just found why initially, waiting 6 seconds, caught a
small number of fines on top of the 75micron sieve.
What is being seen ; theory and practice are matching!
Proceeding onwards:
;; how to never catch 75microns (/ (float 50) ;; 50mm (* (stokes-velocity-pdia dens-silica dens-water visc-water grav-earth 75e-6) mm-per-m) ;; 5.203237320287538 ;; mm s^-1 ) ;; 9.609402170654198 ;; seconds to fall 50mm ;; never catch +75microns if wait more than 10s before ladle to no more than 50mm depth ;; That seems right...
This is what is observed empirically. Wait 10 seconds then ladle the liquid from the near-surface through the sieve and 100% pours straight through, nothing retained on the sieve - yet the water is opaque with suspended fines.
So there we have it:
(R. Smith, 09Aug2025 to 10Aug2025)