
From 21 June 2016 to 12 July 2016 I was gripped by studying the
mathematics of the Finite Element Analysis method.
That was not a development I was expecting!
There was a "long weekend" of catching up with the rest of the world from the end of my 47-day apply a Finite Element Analysis modelling computer-program campaign to 15June2016 ( its closing summary ) to 21 June 2016.
Then this happened!
A 22-day campaign taking a deep interest studying the mathematics
underpinning the computational Finite Element Analysis technique.
This book defined a lot of my world for a while:
"Finite Element Techniques in Structural Mechanics"
(Woodhead Publishing Series in Civil and Structural Engineering)
1 Jan 1996
Carl T. F. Ross (Author)
Paperback: 218 pages

At the time of writing, that book is 20 years old. From back when
Finite Element Analysis was...
rolling out across University engineering courses and pioneering
general engineering companies???
Why and how does this book work for me?
The book restricts itself to constructing the case for Finite Element
Analysis for solely "linear-elastic theory to obtain stresses and
deflections". Solving for increasingly geometrically complex cases
where the material behaviour is "simple" linear-elastic (to an
approximation, "spring-like").
That makes what it has to teach achieveable for someone with an
applied sciences and engineering background. You have the context
knowledge to make the concepts fascinating, engaging and the efforts
immediately rewarding.
The Finite Element Analysis method has been generalised for many
physical systems now and there is a temptation taken up by many
authors to "benefit" the reader with keeping-open that general view.
Making for screeds of new mathematics about which you have no context
knowledge.
Carl Ross understands a group of people he is addressing.
His contributions as a practical engineer are quite widely known.
He's written a book for "us".
Writing this campaign-closing note on 15 July 2016, it remains that no other FEA theory book has worked for me.
Here's some examples to give an overall impression.
Following the examples, you do tens of pages of mathematical
scribblings of the like of the following, which is part of the
learning process...
(miswrote something - about mid-page, should read "2 rows, 2 columns")

(this page does not directly follow on from the previous!)
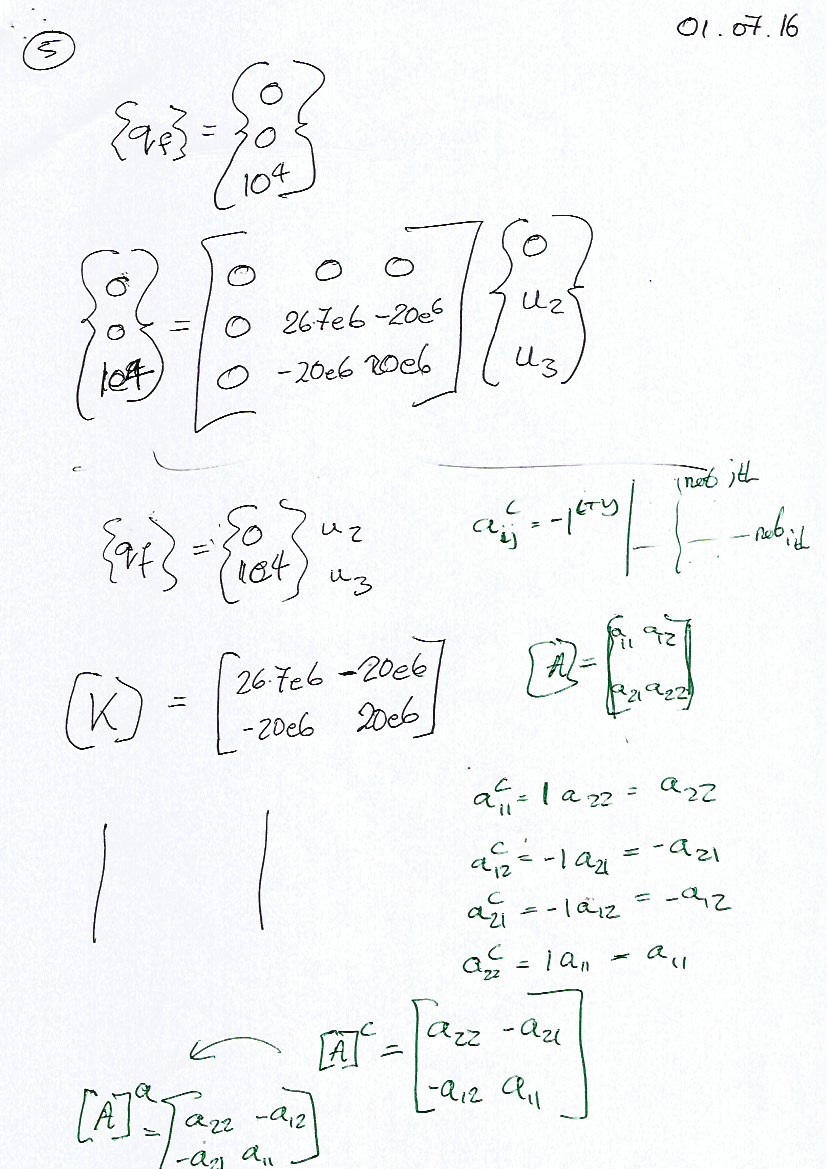
etc
At this level, you do start to see that there is more than one way to do things - your following of the examples becomes more adaptable.
Having done some of the "first-stages teaching" cases from the book on paper, I am already using matrix-arithmetic "generic operations" tools available on-line to rapidly do computationally-intensive steps for larger matrices like
The generic matrix-transformation tools can also be used to do things like multiply the "inverse-matrix" you have derived on-paper by the "original matrix" to see if the answer comes out as the "identity matrix". Which would tend to indicate your derivation is correct.
Finite Element Analysis packages offer analyses of vibration modes.
I thought I'd have to leave that well-alone - at least for now.
Serendipetously - as far as I am concerned - the mathematical study very quickly lead past fundamental matrix mathematical behaviour which makes oscillatory / vibrational modes answers "drop out" as a "bonus-prize" while pursing "shape and forces leads to stresses and deflections" solutions.
I never ever expected I'd be playing with "Eigenvalues" and their
corresponding "Eigenvectors"; with their logic and applications clear.
I'd encountered these terms but assumed they'd always remain "might as
well be written in Gondwanalandish" (ie totally
incomprehensible).
You can very quickly put your derived values back into a
matrix-arithmetic tool and check the answers come out as "unity"
("one") or that the two sides of an equation expressed in matrices are
indeed equal.
It makes the task so much more manageable when a reassuring "quick
check" of being "on-track" only takes a couple of minutes or less.
If this grips you, it's amazing seeing that things like "Eigenvalues and their corresponding Eigenvectors" do indeed have the properties claimed.
No-one who has trodden this path can give you a short-cut to possess
the same view. I am quite sure that is generally true.
You have to tread the path yourself...
During the campaign the sentiment was of: huge efforts for tiny amounts of progress; barely perceptible progress rates; miniscular advancement over previous level of knowledge; etc.
On closing the campaign, that is not the view on looking back at the "terrain" crossed!
The knowledge I have assembled is likely to be retained and persistent - a foundation from which further study can advance.
It's likely that what I have learned will mature in my mind and
develop more strength.
If I get more Trade jobs with repetitive work, I am likely to reflect
and benefit from thinking things through.
If I get Professional / Engineering jobs, it is likely I will find
some application of the knowledge and benefit from mentoring during
the process.
It seems likely that occasionally studying FEA mathematical basis will be a bit of a hobby for while, rather like people do "crossword puzzles" and the like - absorbing intellectual moments.
I've met the "Stiffness Matrix" at the heart of FEA. I've got there
from first principles for "rod" elements in a pin-jointed frame
structure (the nodes don't resist rotation).
Additionally I've seen for 1-D element structures with rigid joints
how that introduces the stiffnesses coming from beam-type resisting of
moments - an additional stiffness.
I have looked ahead to 2-D shell elements ("plate elements") in a full
Finite Element Analysis solution, where I see concepts which are a
continuing draw to revisit.
Bit like how people relate to a holiday location which draws them
back, as much as I understand their feelings from songs, etc
(eg. Chris Rea's "On the Beach").
Onwards, wherever that path may lead...!
(R. Smith, 05Jul2016, 15July2016)